前言

第一章

第二章 连续系统的时域分析

LTI连续系统的响应

一、微分方程的经典解

  • 齐次解（固有响应）
  • 特解（强迫响应）

要求：掌握小于等于三阶的特解和齐次解的结构

二、关于$0_{-}$和$0_{+}$值

若输入信号实在t=0的时刻接入系统

初始值：$y^{(j)}(0_{+})$，直接作为方程的初始值

初始状态：$y^{(j)}(0_{-})$

经典例题：

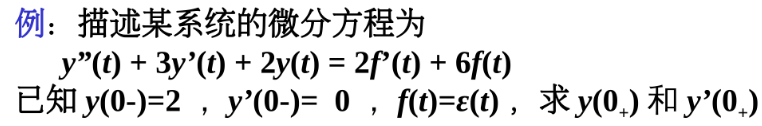
三、零输入响应和零状态响应

对于t=0时接入激励f(t)的系统，初始值：

对于零输入响应，由于激励f(t)为0则有$y_{ZI}^{(j)}(0_-)=y_{ZI}^{(j)}(0_+)=y^{(j)}(0_-)$

对于零状态响应，由于$t=0_-$的时候激励尚未接入，故应有$y_{ZS}^{(j)}(0_-)=0$

则上述式子可以简化为：

经典例题：