高数

写在前面的：

作为一个工科生，高数可谓是十分重要的，在此整理一下高数的知识点，已备后用

---

函数与极限

高数的第一章，定义没什么好讲的，在此记录一下高中没有涉及到的知识点

函数

• 符号函数

  $$y=sgnx=\begin{cases} -1,x<0\\0,x=0\\1,x>0 \end{cases}$$

• 狄利克雷函数

  $$D(x)=\begin{cases} 0,x\in Q \\1,x\in Q^C \end{cases}$$

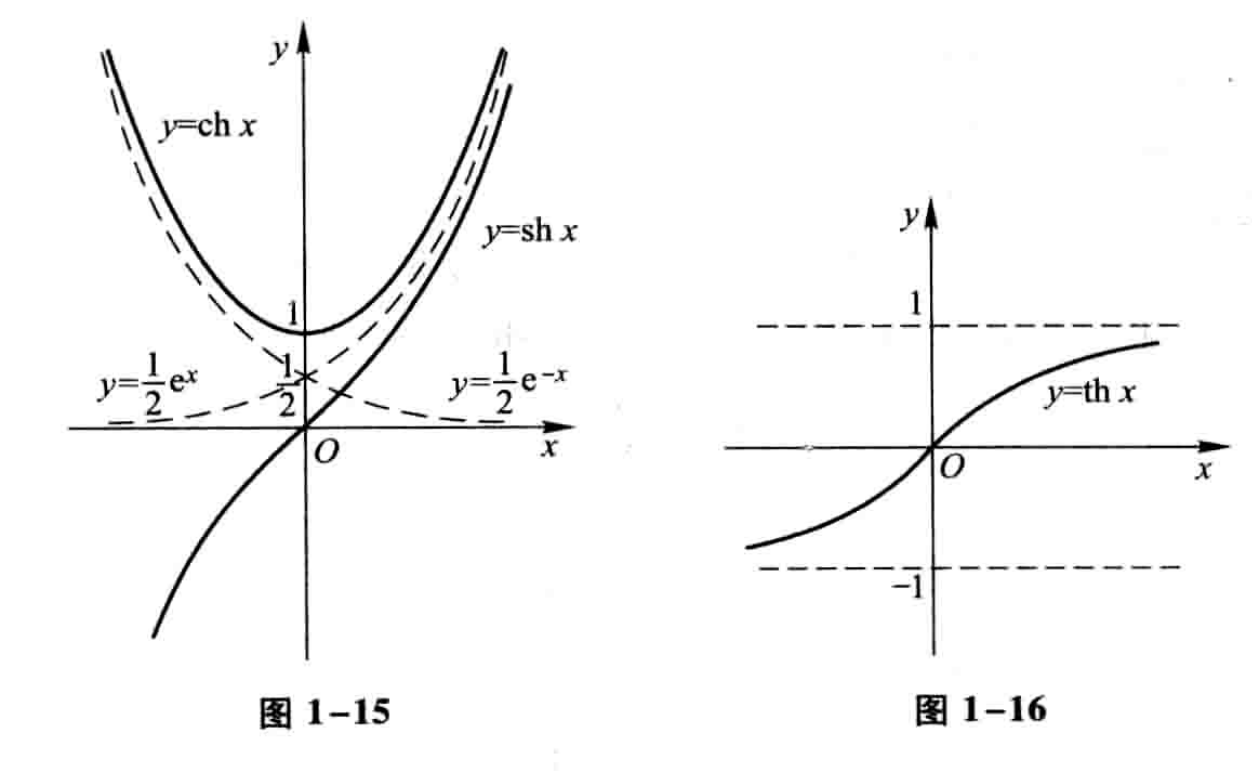
• 双曲函数

  • 双曲正弦

    $$shx=\frac{e^x-e^{-x}}{2}$$

  • 双曲余弦

    $$chx=\frac{e^x+e^{-x}}{2}$$

  • 双曲正切

    $$thx=\frac{shx}{chx}$$

数列

收敛数列的性质

1. 如果数列${x_n}$收敛，那么它的极限唯一
2. 如果数列${x_n}$收敛，那么它一定有界
3. 如果${\lim\limits_{x \to +\infty}}x_n=a$，且$a>0$（或$a<0$），那么存在正整数N，当$n>N$时，都有$x_n>0$(或$x_n<0$)

导数与微分

积分

微分方程

向量与空间解析几何

多元函数微分

重积分

曲线积分与曲面积分

对弧长的曲线积分

1. 定义：

   $$\int_Lf(x,y)ds=\lim\limits_{\lambda \rightarrow 0}\sum_{i=1}^{n}f(\xi_i,\eta_i)$$

2. 计算法

   • 二维

     $$\begin{cases} x=\phi(t)\\ y=\psi(t) \end{cases}$$ $$\int_Lf(x,y)ds=\int_{\alpha}^{\beta}f[\phi(t),\psi(t)]\sqrt{\phi(t)^{'2}+\psi(t)^{'2}}dt$$

• 三维 $$\int_Lf(x,y,z)ds=\int_{\alpha}^{\beta}f[\phi(t),\psi(t),\omega(t)]\sqrt{\phi(t)^{'2}+\psi(t)^{'2}+\omega(t)^{'2}}dt$$

对坐标曲线的积分

1. 定义

2. 计算法

   $$\int_LP(x,y)dx+Q(x,y)dy=\int_{\alpha}^{\beta}\{P[\phi(t),\psi(t)]\phi^{'}(t)+Q[\phi(t),\psi(t)]\psi^{'}(t)\}dt$$

两类曲线积分的联系

• 二维

  $$\int_LPdx+Qdy=\int_L(Pcos\alpha+Q\cos\beta)ds$$

• 三维

  $$\int_LPdx+Qdy+Rdz=\int_L(Pcos\alpha+Q\cos\beta+Rcos\gamma)ds$$

格林公式

1. 格林公式：

   $$\iint_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\oint_LPdx+Qdy$$

   其中，L是D的正向的边界曲线

2. 曲线积分与路径无关的条件

   $$\frac{\partial Q}{\partial x}=\frac{\partial P}{dy}$$

对面积的曲面积分

1. 定义

2. 计算法

   $$\iint_\sum f(x,y,z)dS=\iint_{Dxy}f[x,y,z(x,y)]\sqrt{1+z_x^2(x,y)+z_y^2(x,y)}dxdy$$

对坐标的曲面积分

1. 定义

2. 计算法

   $$\iint_\sum R(x,y,z)dxdy=\iint_{Dxy}R[x,y,z(x,y)]dxdy$$

两类曲面积分的联系

$$\iint_{\sum}Pdydz+Qdzdx+Rdxdy=\iint_{\sum}(Pcos\alpha+Q\cos\beta+Rcos\gamma)dS$$

高斯公式

$$\iiint \limits_{\Omega}(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dv=\oiint \limits_{\sum}Pdydz+Qdzdx+Rdxdy$$

无穷级数

常数项级数的概念和性质

级数的定义：

$$\sum \limits_{i=1} ^{\infty}u_i=u_1+u_2+\cdots+u_i+\cdots$$

部分和：

$$s_n=\sum \limits_{i=1} ^{n}u_i$$

收敛级数：

1. 定义：

   $$\lim \limits_{n\rightarrow\infty}s_n=s$$

2. 性质：

   • 如果级数$\sum \limits_{n=1}^{\infty}u_n$收敛于和$s$，那么级数$\sum \limits_{n=1}^{\infty}ku_n$也收敛，且其和为$ks$
   • 如果级数$\sum \limits_{n=1}^{\infty}u_n$和$\sum \limits_{n=1}^{\infty}v_n$分别收敛于和$s与\sigma$，那么级数$\sum \limits_{n=1}^{\infty}(u_n\pm v_n)$也收敛，且其和为$s+\sigma$
   • 在级数中去掉、加上或改变有限项，不会改变级数的收敛性
   • 如果级数收敛，那么它的一般项趋于0

常数项级数的审敛法