写在前面的：

由于半个学期不到电路基础就上完了，期中考试又是电路的期末，在此梳理一些电路课本中的重要知识，以备后用。

Chapter1

齐次定理

描述：对于具有唯一解的线性电路，当只有一个激励源（独立电压源或独立电流源）作用的时候，其响应（电路任意处的电压或电流）与激励成正比。

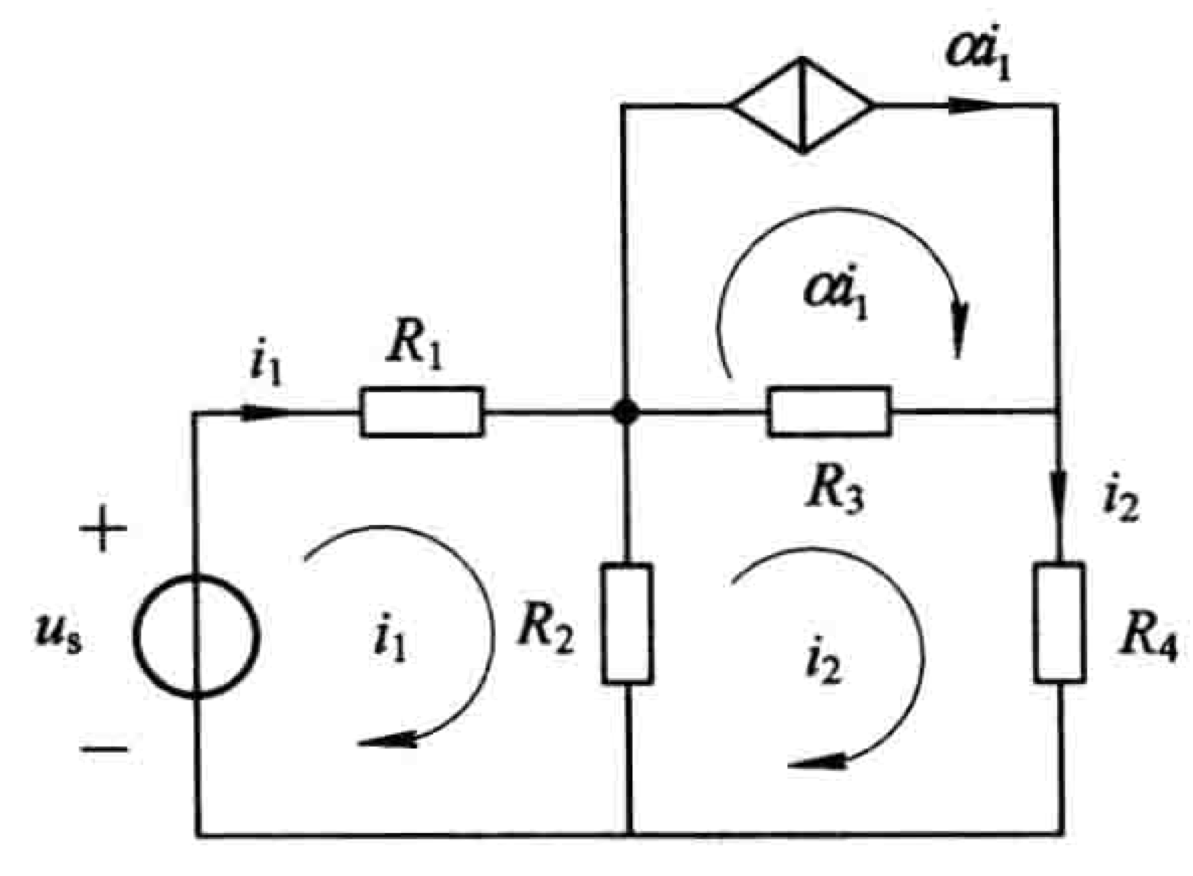
上述例子使用网孔法得

$\begin{cases} (R_1+R_2)i_1-R_2i_2=u_s \\ -\alpha R_3i_1-R_2i_1+(R_2+R_3+R_4)i_2=0 \end{cases}$

叠加定理

描述：对于具有唯一解的线性电路，多个激励源共同作用时引起的响应（电路中各处的电流电压）等于各个激励源单独作用（其他激励源置零）时所引起的响应之和。

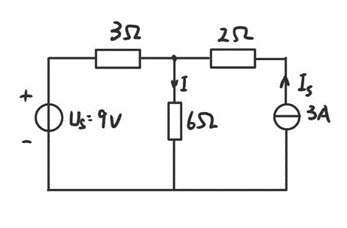
试计算电流I：

利用叠加定理：将电流源断路， $I_1=1 A$，将电压源短路，$I_2=1 A$。

则：$I=I_1+I_2=2 A$

替代定理

戴维南等效

描述：任意一个线性一端口电路N，它对外电路的作用可以用一个电压源和电阻的串联组合来等效。该电压源的电压Uoc等于一端口电路在端口出的开路电压；电阻R0等于一端口电路内所有独立源置为0的条件下，从端口看进去的等效电阻。

计算等效电阻的方法：

有无受控源
- 无受控源：串并联方法
- 有受控源：
  - 外加电源法：所有的独立源置零，保留受控源，R=U/I
  - 开路短路法：$R=U_{oc}/I_{sc}$
  - 伏安关系法：$U=U_{oc}+IR_0$

计算开路电压的方法:

负载支路断开，设出开路电压$u_{oc}$的参考方向，计算$u_{oc}$

计算短路电流的方法:

负载支路短路，设出短路电流$i_{sc}$的参考方向，计算$i_{sc}$

最大功率传输条件

当且仅当负载电阻等于戴维宁等效内阻时，功率最大。

$P_{max}=\frac{u_{oc}^2}{4R_0}(R_L=R_0)$

Chapter2

电容

电容是一种存储电能的元件

单位：F（法）

$C=\frac{q(t)}{u(t)}$

电容的VAR

$i(t)=C\frac{du}{dt}$

如果电容的电压和电流采用非联参考方向：

$i(t)=-C\frac{du}{dt}$

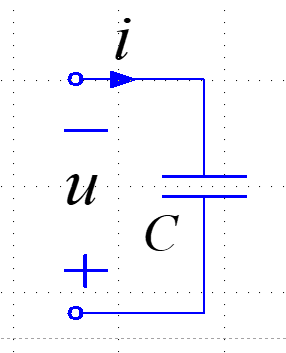
电容的功率 $p(t)=i(t)u(t)$

当$p(t)>0$ 电容吸收能量，处于充电状态
当$p(t)<0$ 电容放出能量，处于放电状态

电容的储能：

$w_c(t)=\frac{1}{2}Cu^2(t)$

电感

电感式一种存储磁能的元件

单位：H（亨）

$L=\frac{\Psi (t)}{i(t)}$

电感的VAR

$u(t)=L\frac{di}{dt}$

如果电感的电压和电流采用非联参考方向：

$u(t)=-L\frac{di}{dt}$

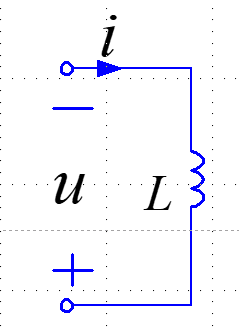
电感的功率 $p(t)=i(t)u(t)$

当$p(t)>0$ 电感吸收能量，处于充磁状态
当$p(t)<0$ 电感放出能量，处于放磁状态

电感的储能：

$w_L(t)=\frac{1}{2}Li^2(t)$

以下仅适用于$u_{c}(0^+)和i_L(0^+)$

零输入响应

定义：外加激励均为0时，仅由初始状态引起的响应

$y(t)=y(0_+)e^{-\frac{t}{\tau}}$

零状态响应

定义：当电路的初时储能为零时，仅由外加的激励所引起的响应

$y(t)=y(\infty)[1-e^{-\frac{t}{\tau}}]\$

全响应公式

$y(t)=[y(0_+)-y(\infty)]e^{-\frac{t}{\tau}}+y(\infty)$ $\tau=\frac{L}{R}=RC$

PS:值得注意的是，以上公式只是用与直流激励下的一阶电路任意出的电流和电压

Chapter3

正弦量

瞬时值表达式

$i(t)=I_mcos(\omega t+\phi_i)$ $u(t)=U_mcos(\omega t+\phi_i)$

三要素：

振幅 $U_m、I_m$
角频率 $\omega$
初相 $\phi_i$

有效值：

$I=\sqrt{\frac{1}{T} \int_0^T{i^2(t)dt}} \qquad U=\sqrt{\frac{1}{T} \int_0^T{u^2(t)dt}}$ $I=\frac{I_m}{\sqrt{2}} \qquad U=\frac{U_m}{\sqrt{2}}$

PS:平时所说的正弦交流电的大小指的都是有效值，如：民用交流电压220V

相量

使用范围：同频率的正弦量之间的运算

为什么要用相量表示正弦量：为了简便运算

构造一个复函数 $A(t)=\sqrt{2}Ie^{j(\omega t+\phi)}=\sqrt{2}Icos(\omega t+\phi)+j\sqrt{2}Isin(\omega t+\phi)$

其中的实部是一个正弦量

其中 $A(t)$ 还可以写成一下形式：

$A(t)=\sqrt{2}Ie^{j\phi}e^{j\omega t}$

可以定义一个复常数 $\dot{I}=Ie^{j\phi}=I\angle\phi_i$

相量的运算

相量的加减

$\dot{U}=\dot{U_1}+\dot{U_2}$

相量的微积分运算

$\frac{di(t)}{dt}\leftarrow\rightarrow j\omega\dot{I}$ $\int i(t)dt\leftarrow\rightarrow \frac{\dot{I}}{j\omega}$

阻抗

$Z=\frac{\dot{U}}{\dot{I}}=\lvert Z\rvert\angle\theta_Z=R+jX$

阻抗模 $\lvert Z\rvert=\frac{U}{I}=\sqrt{R^2+X^2}$
阻抗角 $\theta_Z=\phi_u-\phi_i=arctan\frac{X}{R}$

功率

瞬时功率

$p(t)=u(t)i(t)$

平均功率（有功功率）

$P=UIcos\theta$

单位：瓦（W）

$\theta=\phi_u-\phi_i$ 称为功率因数角

$cos\theta$ 称为功率因数

无功功率Q

$Q=UIsin\theta$

单位：乏(var)

实际意义：反应电路N与外电路交换功率的大小，有储能元件L、C决定

视在功率S

$S=UI$

单位：伏安（VA）

实际意义：反应电器设备的容量

最大功率传输条件

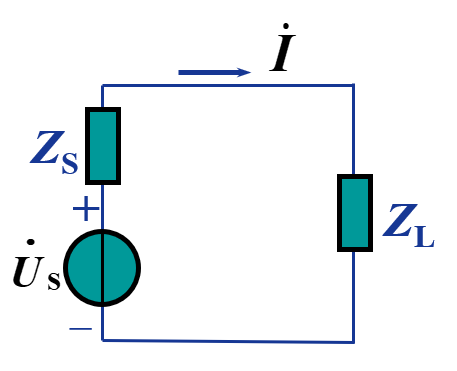
我们来讨论一下正弦稳态电路中的负载 $Z_L$ 获得最大功率 $P_{max}$ 的条件

不妨设 $Z_S=R_S+jX_S \quad Z_S=R_S+jX_S$

则有 $\dot{I}=\frac{\dot{U_s}}{Z_S+Z_L} \quad I=\frac{U_s}{\sqrt{(R_S+R_L)^2+(X_R+X_L)^2}}$

如果 $Z_L=R_L+jX_L$ 可以任意改变(共轭匹配)
$P_{max}=\frac{U_s^2}{4R_s}$
条件：
$\begin{cases} R_L=R_S\\ X_L=-X_S \end{cases}$
如果 $Z_L=R_L+jX_L=\lvert Z\rvert \angle \theta$ 其中 $\lvert Z_L\rvert$ 可以任意改变，但是 $\theta$ 不变（模匹配）
$P_{max}=\frac{cos\theta U_S^2}{2\lvert Z \rvert + 2(R_Scos\theta+X_Ssin\theta)}$
条件：
$\lvert Z_S\rvert = \lvert Z_L\rvert$

互感耦合电路

耦合电感

但有一个线圈中通有电流时，在自身中激发自磁通，其中有一部分通过另外一个线圈，称为互磁通。

耦合系数k（用于描述两个线圈耦合的松紧程度）

$k=\sqrt{\frac{\Phi_{21}}{\Phi_{11}}\frac{\Phi_{12}}{\Phi_{22}}}=\frac{M}{\sqrt{L_1L_2}}$

无耦合：k=0,M=0，两个线圈互不影响
全耦合：k=1

同名端：当电流从两线圈各自的某端子同时流入(或同时流出)时，若两线圈产生的磁通相助

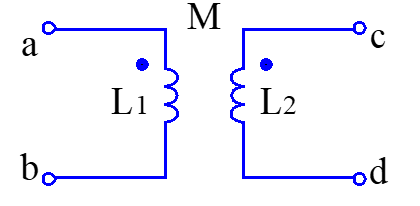
异名端：当电流从两线圈各自的某端子同时流入(或同时流出)时，若两线圈产生的磁通相消

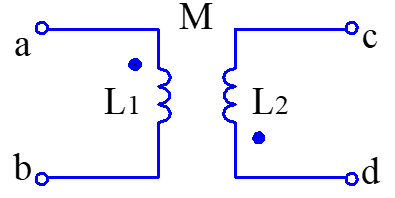
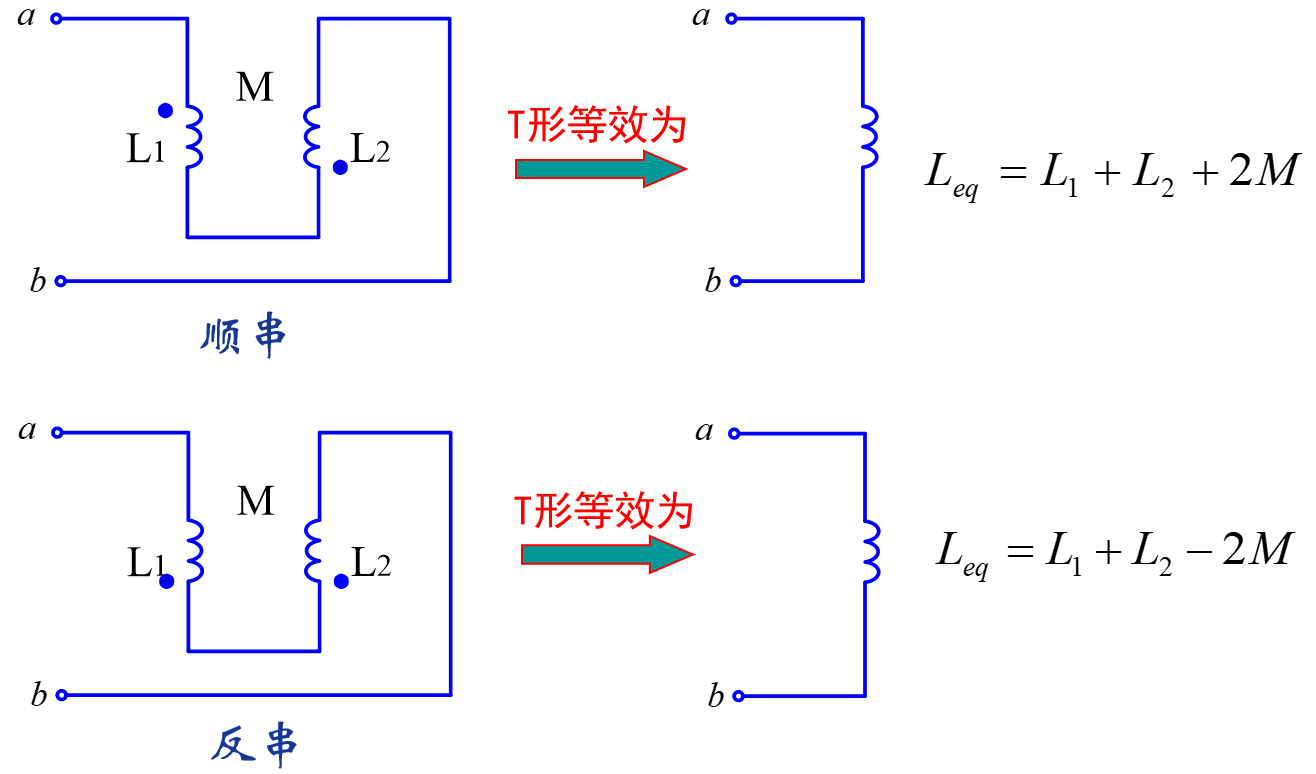
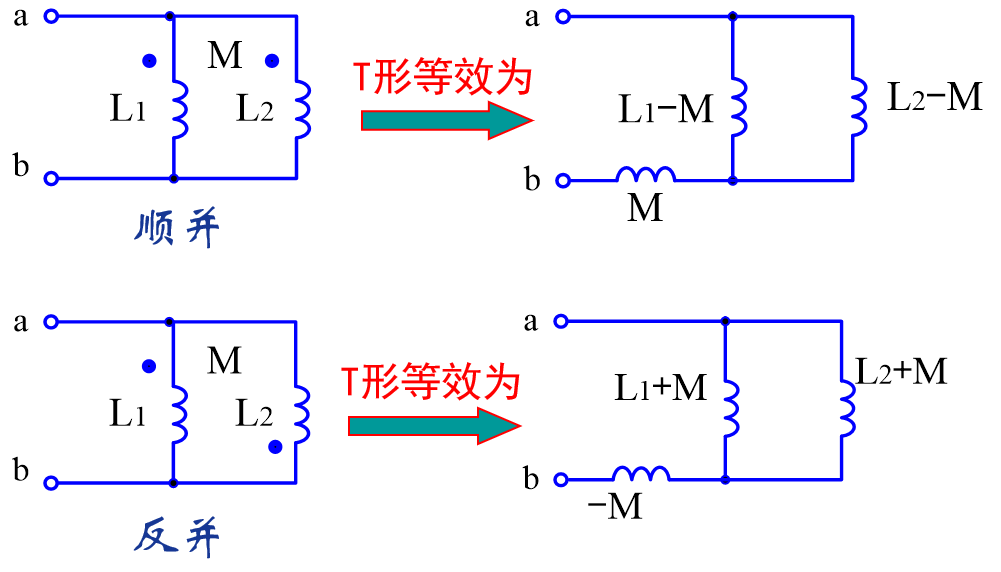
T型去耦等效

同名端等效：

异名端等效：

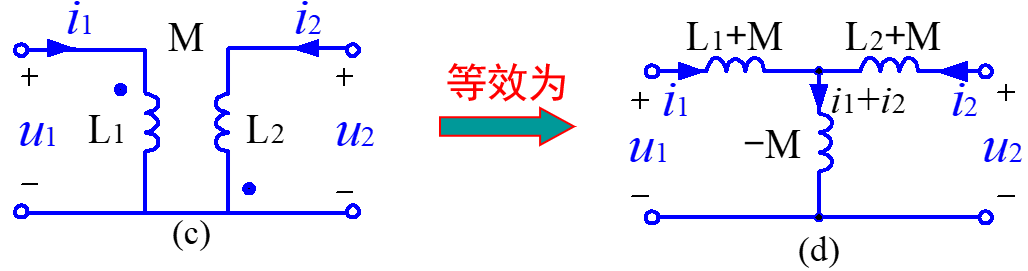
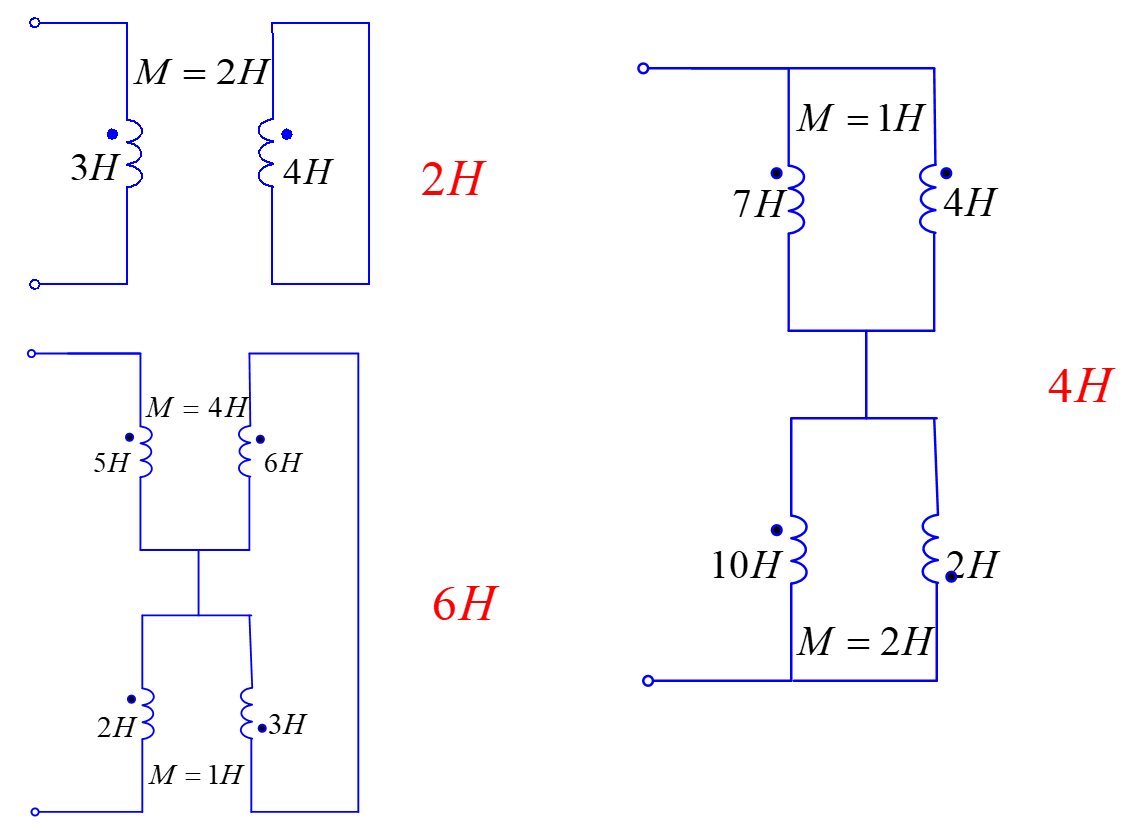
几个T型去耦等效的例子

变压器

理想变压器

条件：

全耦合,k=1
自感$L_1、L_2\rightarrow \infty$,且$\frac{L_1}{L_2}$为常数
无损耗

特性：

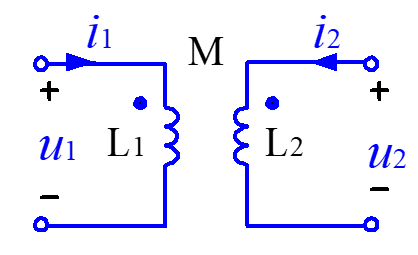
$n=\frac{N_1}{N_2}$

变压特性
$\frac{u_1}{u_2}=\frac{N_1}{N_2}=n$

PS:如果是异名端，则$\frac{u_1}{u_2}=-\frac{N_1}{N_2}=-n$
变流特性
$i_1(t)=-\frac{N_2}{N_1}i_2(t)=-\frac{1}{n}i_2(t)$

PS:如果是异名端，则$i_1(t)=\frac{N_2}{N_1}i_2(t)=\frac{1}{n}i_2(t)$
变阻特性
$Z_{in}=(\frac{N_1}{N_2})^2Z_L=n^2Z_L$

PS:变阻特性与同名端一名端没有关系

Chapter4

频率响应与网络函数

网络函数是用来描述电路的频率特性

$H(j\omega)=\frac{响应相量\dot{Y}}{激励相量\dot{F}}$

网络函数一般是$\omega$的复函数，亦可写作：

$H(j\omega)=\lvert H(j\omega)\rvert e^{j\theta(\omega)}$

幅频特性

相频特性

一阶电路的频率响应

串联谐振电路

RLC串联谐振

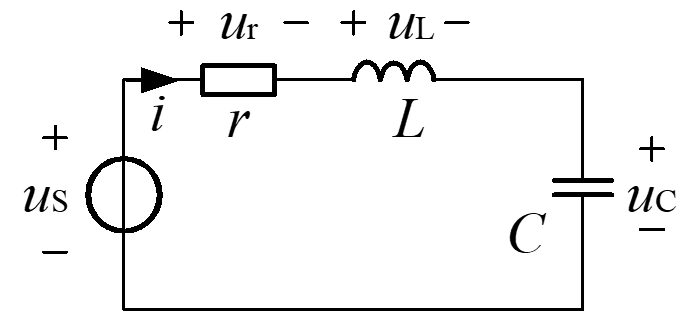
总阻抗：$Z=r+jX=r+j(\omega L-\frac{1}{\omega C})$

谐振概念：当电源频率改变到摸一个值时，会使$X=0$则称谐振电路发生了串联谐振

谐振角频率：$\omega_0=\frac{1}{\sqrt{LC}} $

特性阻抗：电路在发生谐振是感抗和容抗在数值上相等

$\rho=\omega_0 L=\frac{1}{\omega_0 C}=\sqrt{\frac{L}{C}}$

品质因数：电路的特性阻抗与回路的电阻比值

$Q=\frac{\rho}{r}=\frac{\omega_0 L}{r}=\frac{1}{\omega_0 Cr}$

在此区分一下电路的品质因数和原件的品质因数的区别：

元件的品质因数：

$Q=2\pi \frac{储能的最大值}{一周期的耗能}$

通频带：

$B=\frac{\omega_0}{Q}=\frac{r}{L}$

并联谐振电路

GCL并联谐振

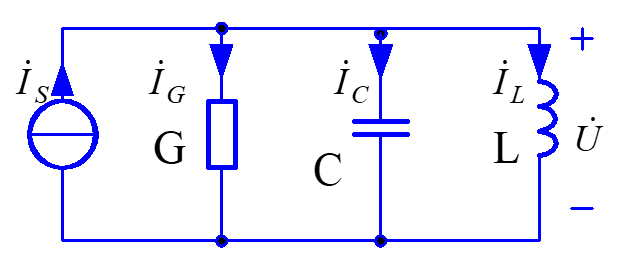
总阻抗：$Y=G+jB=G+j(\omega C-\frac{1}{\omega L})$

谐振角频率：$\omega_0=\frac{1}{\sqrt{LC}} $

特性阻抗：电路在发生谐振是感抗和容抗在数值上相等

$\rho=\omega_0 L=\frac{1}{\omega_0 C}=\sqrt{\frac{L}{C}}$

品质因数：电路回路的电阻与特性阻抗的比值

$Q=\frac{r}{\rho}=\frac{\omega_0 C}{G}=\omega_0CR=\frac{R}{\omega_0 L}$

通频带：

$B=\frac{\omega_0}{Q}=\frac{1}{RC}$

简单的并联谐振电路

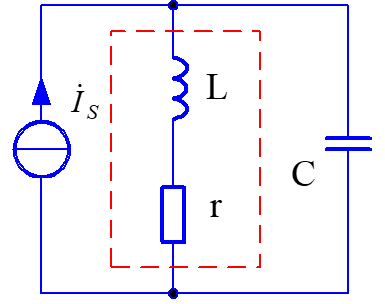
在实际工程的谐振电路中，电感线圈的孙高相对于电容影响较大，因此，工程上的电感通常可以堪称是一个理想电感和一个电阻串联而成。此外，谐振电路一般工作在谐振频率附近，并且Q值较高（Q>>1）。

在以上的情况下，这种实际的并联谐振电路可以等效成上述的一般的并联谐振电路形式。

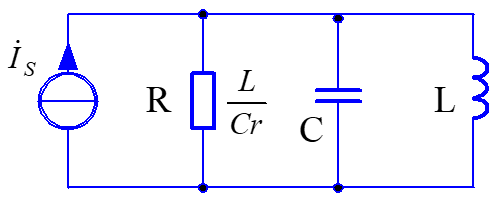
谐振频率：若$r<<\omega_0L$，则$\omega \approx \sqrt{\frac{1}{LC}}$

谐振阻抗：$Z_0=R=\frac{L}{Cr}$

品质因数：$Q=\frac{R}{\omega_0L}=\frac{\omega_0L}{r}$

PS：关于为什么并联谐振的品质因数是串联的倒数，可以看关于品质因数的具体定义

复杂的并联谐振电路

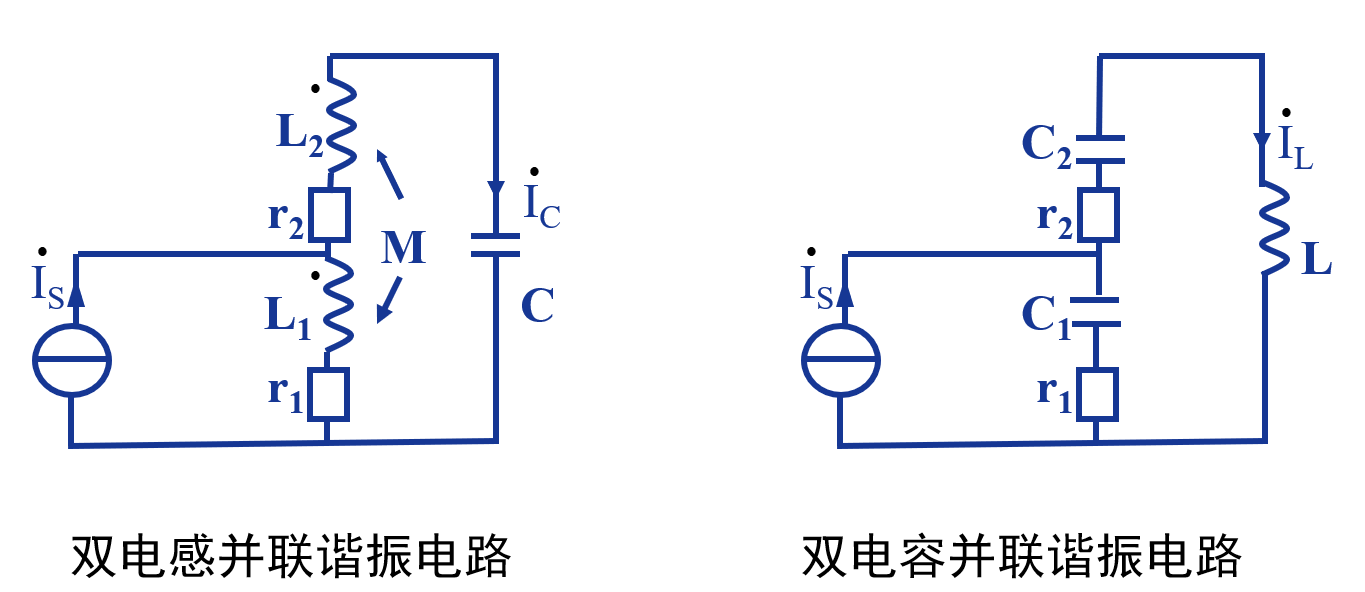
上述的两个复杂并联谐振电路均可等效成为以下的电路：

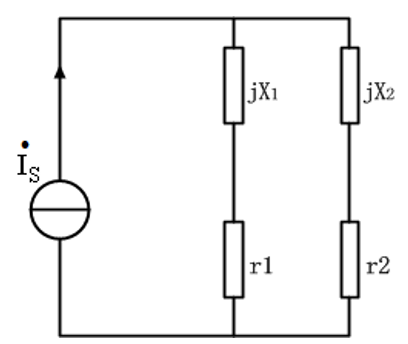
电路的总导纳：

$Y=\frac{1}{r_1+jX_1}+\frac{1}{r_2+jX_2}=[\frac{r_1}{r_1^2+X_1^2}+\frac{r_2}{r_2^2+X_2^2}]-j[\frac{X_1}{r_1^2+X_1^2}+\frac{X_2}{r_2^2+X_2^2}]$

由于电路的Q值较高，即：$r_1^2<<X_1^2,r_2^2<<X_2^2$，则上述总到哪可以化简成：

$Y\approx [\frac{r_1}{X_1^2}+\frac{r_2}{X_2^2}]-j[\frac{1}{X_1}+\frac{1}{X_2}]$

当电路发生谐振时，总电纳等于0，即：

$\frac{1}{X_1}+\frac{1}{X_2}=0 \rightarrow X_1+X_2=0$

上式说明了复杂并联谐振电路谐振时仍然是总电抗等于零

那么就有复杂并联谐振电路的角频率：

$\omega_0=\frac{1}{\sqrt{LC}}$

其中，L为总电感，C为总电容

高Q值双电感并联谐振电路
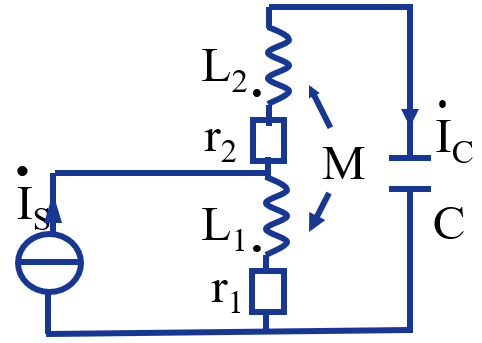
- 有互感
  
  $\omega_0=\frac{1}{\sqrt{(L_1+L_2+2M)C}}$
- 无互感
  
  $\omega_0=\frac{1}{\sqrt{(L_1+L_2)C}}$
  
  此外，$L_2和C$也可以发生串联谐振，其谐振频率表为：$\omega_{03}=\frac{1}{L_2C}$

高Q值双电容并联谐振电路

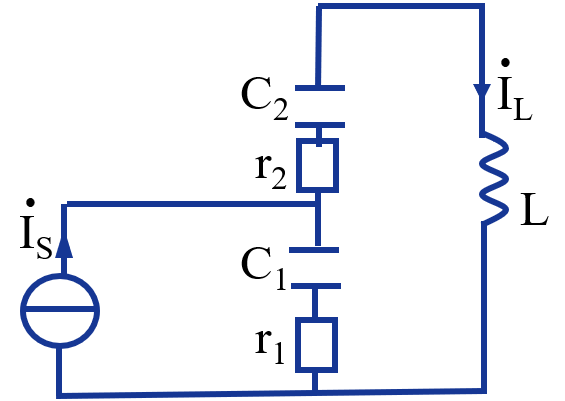
$\omega_0=\frac{1}{\sqrt{L\frac{C_1C_2}{C_1+C_2}}}$

补充：

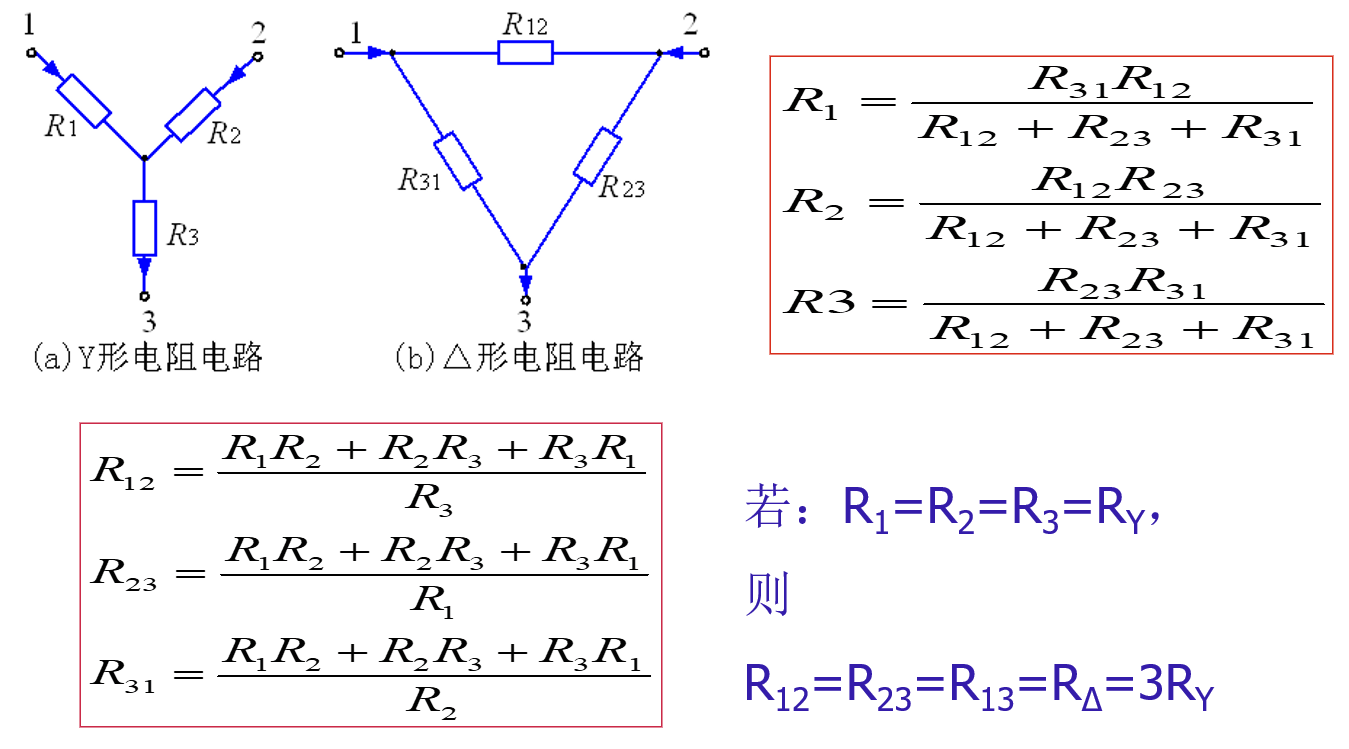
纯电阻电路的$Y-\Delta$变换